Frans Susilo, SJ

Program Studi Matematika, Fakultas Sains dan Teknologi,

Universitas Sanata Dharma

Alamat e-mail: fsusilo@usd.ac.id

1.     Pendahuluan

Tidak dapat disangkal bahwa salah satu komponen penting dalam matematika mo­dern dewasa ini adalah Teori Himpunan. Semua struktur dalam matematika pada dasarnya adalah suatu himpunan, misalnya struktur himpunan semua bilangan real, struktur gelanggang dan ruang vektor yang adalah suatu himpunan dengan dua operasi dan memenuhi persyaratan tertentu, struktur topologi yang dibangun atas dasar himpun­an-himpunan ter­buka, dsb. Konsep-konsep dasar dalam matematika didefinisikan dengan menggunakan konsep himpunan, misalnya konsep bangun dalam geometri sebagai him­punan titik-titik dalam bidang atau ruang, konsep relasi dan fungsi sebagai himpunan bagian dari suatu himpunan darab Cartesius, dan konsep operasi, barisan, dan determinan sebagai fungsi, yang berarti dapat didefinisikan sebagai himpunan. Peranan mendasar yang demikian itu menempatkan Teori Himpunan sebagai salah satu komponen terpen­ting dalam Landasan Matematika.

Teori Himpunan dirintis dan dikembangkan oleh matematikawan Jerman, Georg Cantor (1845 – 1918), menjelang akhir abad sembilan belas. Cantor mendefinisikan “himpunan” (set) sebagai koleksi obyek-obyek dari pikiran atau intuisi kita yang tertentu dan terbedakan satu sama lain dan yang dipandang sebagai suatu kesatuan. Teori Him­punan selanjutnya berkembang dengan pesat dan berfungsi sebagai landasan dan bahasa matematika. Namun ditemukannya beberapa paradoks (suatu pernyataan yang menim­bulkan kontradiksi) dalam Teori Him­punan pada awal abad dua puluh (misalnya para­doks Russell, paradoks Burali-Forti, paradoks Richard, dll) sempat menggoyahkan kedudukan teori baru Cantor tersebut. Keadaan tersebut mendorong para mate­matikawan dari berbagai kalangan untuk menyelamatkan Teori Himpunan itu dengan menggunakan pendekatan yang lebih sistematis dan dengan pola deduktif, yaitu dengan membangun kembali Teori Himpunan secara aksiomatis. Hasil­nya adalah Teori Himpunan aksiomatik yang terbebas dari bahaya kontradiksi, antara lain Teori Himpunan Zermelo-Fraenkel (ZF) dan Teori Himpunan Von Neumann-Bernays-Gödel (NBG). Berkat Teori Himpunan matematika dapat berkembang secara pesat dan menjadi lebih akurat. Konsep-konsep dalam matematika yang semula hanya dipahami secara intuitif dapat dirumuskan secara lebih tepat dengan menggunakan konsep himpunan.

 Gambar 1. Georg Cantor

Namun demikian, realitas dunia nyata yang menjadi ajang pergumulan ilmu memiliki kompleksitas yang sedemikian tinggi dan unsur-unsur yang sedemikian kaya, sehingga matematika yang sudah berkem­bang semakin canggih sekalipun hanya dapat menangkap, memodelkan, dan meng­analisis sebagian (kecil) saja dari realitas itu. Masih banyak unsur dalam realitas dunia nyata itu yang tidak mampu disentuh oleh matematika. Para ahli matematika terus menerus berusaha untuk mencari terobosan guna mengatasi keterbatasan matematika itu.

2.     Pengembangan Teori Himpunan

Tugas ilmu pengetahuan, termasuk matematika, antara lain adalah untuk menye­lidiki, menganalisis, dan mempelajari ge­jala-gejala yang dialami oleh manusia dalam ke­hidupannya. Hal itu dilakukan dengan menciptakan model-model yang sesuai dan ke­mudian menganalisis serta memanipulasi model-model itu dengan berbagai perangkat keilmuan yang tersedia. Model yang disusun dalam matematika tradisional adalah model yang didasarkan pada logika dan himpunan yang tegas, yaitu himpunan dengan batas yang tegas antara elemen-elemen yang merupakan anggota suatu himpunan dan elemen-elemen yang bukan anggota himpunan itu (berarti pula batas yang tegas antara pernyata­an yang benar dan pernyataan yang salah). Banyak gejala di dunia nyata yang tidak mu­dah dan bahkan tidak mungkin untuk disusun modelnya dengan perangkat yang tersedia dalam matematika klasik karena gejala itu secara intrinsik tidak bersifat hitam-putih se­cara tegas, melainkan mengan­dung unsur-unsur kekaburan, ketidakpastian dan/atau keti­daktegasan. Dalam beberapa dekade terakhir ini telah dikembangkan berbagai teori baru untuk menyele­saikan masalah-masalah dunia nyata yang memuat ketidakpastian, keka­buran, ketidak­tegasan yang tidak dapat diselesaikan dengan menggunakan konsep-konsep dan metode-metode kon­vensional yang sudah dikenal dalam mate­matika.

Teori peluang (Probability Theory) selama ini (sejak abad tujuh belas) merupakan satu-satunya metode mate­matika yang dipergunakan untuk memecahkan masalah keti­dakpastian itu, khususnya keti­dakpastian yang bersifat acak (random). Usaha untuk menangani masalah ketidakpastian jenis lainnya baru terwujud pada tahun 1965 ketika Lotfi A. Zadeh (saat ini berusia 92 tahun) memperkenalkan teori Himpunan Kabur (Fuzzy Sets), yang menghasilkan model untuk menyelidiki gejala kekaburan semantik dengan menggunakan konsep variabel linguistik dan fungsi keanggotaan.

Gambar 2. Lotfi A. Zadeh

Kemudian pada tahun 1982 matematikawan Polandia, Zdzislaw Pawlak (1926 – 2006), memperkenalkan teori Himpunan Kasar (Rough Sets) yang dikembangkan untuk menggarap masalah keti­dakpastian atas dasar konsep partisi dan ruang hampiran yang di­bangkitkan oleh suatu relasi ekivalensi.

Gambar 3. Zdzislaw Pawlak

Selanjut­nya untuk mengatasi keterbatasan yang me­lekat pada kedua teori baru tersebut terutama karena kurangnya parameterisasi, seorang matematikawan Rusia, Dmitri A. Molodtsov, pada tahun 1999 memperkenalkan suatu pendekatan yang berbeda dengan menggunakan konsep baru yang disebutnya Himpunan Lunak (Soft Sets). Kalau him­punan ka­bur dikembangkan de­ngan menggunakan fungsi keanggotaan dan himpunan kasar ber­dasarkan relasi ekivalensi dan partisi, maka himpunan lunak didefinisikan ber­dasarkan apa yang oleh Molodtsov disebut him­punan pa­rameter.

3.      Teori Himpunan Kabur

Himpunan yang didefinisikan oleh Cantor seringkali disebut himpunan tegas (crisp set), karena terdapat batas yang tegas antara unsur-unsur yang merupakan anggota dan unsur-unsur yang tidak merupakan anggota dari suatu himpunan. Tetapi dalam ke­nyataan­nya tidak semua himpunan yang kita jumpai dalam kehidupan sehari-hari terde­finisi secara demikian tegas itu, misalnya himpunan orang miskin, himpunan mahasiswa pandai, himpunan orang yang tinggi, dsb. Pada himpunan orang yang tinggi, misalnya, kita tidak dapat me­nentukan secara tegas apakah seseorang adalah tinggi atau tidak. Kalau misalnya kita de­finisikan bahwa “orang tinggi” adalah orang yang tingginya lebih besar atau sama dengan 2 meter, maka seorang yang tingginya 1.99 meter menurut de­finisi tersebut termasuk orang yang tidak tinggi. Sulit bagi kita untuk menerima bahwa orang yang tingginya 1.99 meter itu tidak termasuk orang yang tinggi. Hal itu menunjuk­kan bahwa memang batas antara kelompok orang tinggi dan kelompok orang tidak tinggi tidak dapat ditentukan se­cara tegas.

Untuk mengatasi permasalahan himpunan dengan batas yang tidak tegas itu, Zadeh memperkenal konsep himpunan kabur (fuzzy sets) dengan cara mengaitkan him­punan semacam itu dengan suatu fungsi yang menyatakan derajat kesesuaian unsur-unsur dalam semestanya dengan konsep yang merupakan syarat keang­gotaan himpunan terse­but. Fungsi itu disebut fungsi keanggotaan dan nilai fungsi itu dise­but derajat keanggo­taan suatu unsur dalam himpunan itu. Dengan demikian setiap unsur dalam semesta wacananya mem­punyai derajat keanggotaan tertentu dalam himpunan tersebut yang di­nyatakan dengan suatu bilangan real dalam selang tertutup [0,1]. Fungsi keanggotaan dari suatu himpunan kabur  dalam semesta X adalah pemetaaan  Nilai fungsi  menyatakan derajat keang­gotaan unsur  dalam himpunan kabur . Nilai fungsi sama dengan 1 menyata­kan keanggotaan penuh, dan nilai fungsi sama de­ngan 0 menyatakan samasekali bukan anggota himpunan kabur tersebut. Maka himpunan tegas juga dapat dipandang sebagai kejadian khusus dari himpunan kabur, yaitu himpun­an ka­bur yang fungsi keang­gotaannya hanya bernilai 0 atau 1 saja.

Himpunan orang yang tinggi itu, misalnya, dapat dinyatakan dengan fungsi keang­gotaan  dengan grafik seperti disajikan dalam Gambar 4.

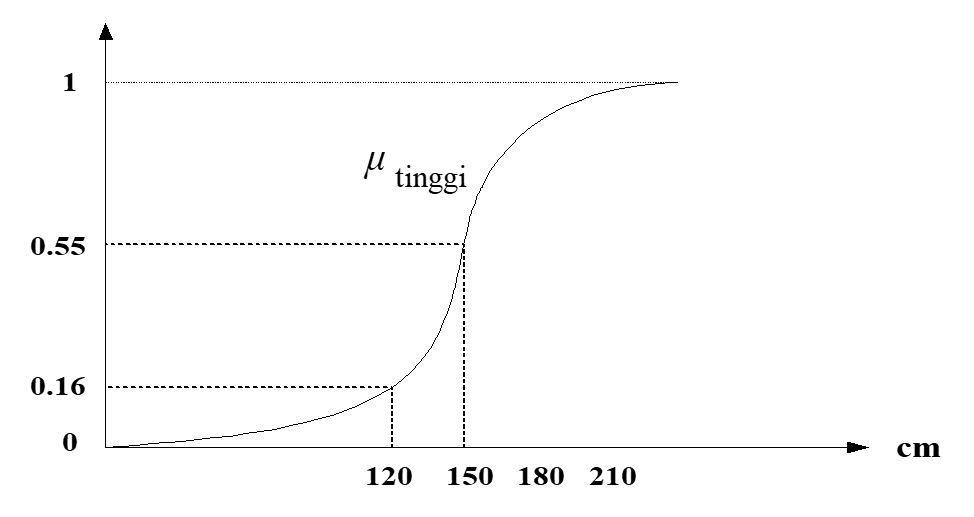
Gambar 4. Fungsi keanggotaan himpunan kabur “tinggi”

Misalnya seseorang yang tingginya 120 cm mempunyai derajat keanggotaan 0.16, yaitu  dan seseorang yang tingginya 150 cm mempunyai derajat keang­gotaan 0.55, yaitu  dalam himpunan kabur “tinggi” tersebut.

4.      Teori Himpunan Kasar

Himpunan kasar (rough sets) pertama kali diperkenalkan oleh Zdzislaw Pawlak pada tahun 1982 sebagai suatu metode matematis untuk mendeskripsikan himpunan tidak tegas, dalam arti bahwa elemen-elemen tertentu dalam semestanya tidak dapat ditentukan secara tegas apakah merupakan anggota himpunan itu atau tidak karena elemen-elemen itu tidak dapat dibedakan satu sama lain akibat keterbatasan atau ketidaklengkapan pe­ngetahuan atau informasi yang tersedia mengenai elemen-elemen itu. Himpunan kabur yang dikembangkan oleh Zadeh menangani kekaburan semantik dari konsep-konsep yang tidak dapat didefinisikan secara tegas, sedangkan him­punan kasar Pawlak ini menangani ketidaktegasan yang disebabkan oleh takter­bedakannya elemen-elemen tertentu dalam semesta himpunan itu. Kedua konsep himpunan tak-tegas itu memang berbeda karena menanggapi dua jenis ketidaktegasan yang berbeda.

Pada awalnya himpunan kasar dikembangkan untuk menangani ketidakpastian dan ketidaktegasan dalam bidang analisis data. Dasar pengembangan teori himpunan ka­sar adalah asumsi bahwa setiap elemen dalam semesta wacananya terkait dengan infor­masi mengenai elemen itu, dan bahwa elemen-elemen dengan informasi yang sama adalah elemen-elemen yang takterbedakan. Pada dasarnya pendekatan terhadap him­punan kasar adalah suatu hampiran terhadap himpunan tak­-tegas itu dengan meng­guna­kan sepasang himpunan tegas yang dikonstruksikan berdasarkan suatu partisi pada se­mesta himpunan itu. Sebagai partisi biasanya diambil partisi yang dibangkitkan oleh re­lasi ekivalensi “takterbedakan” antara elemen-elemen dalam semesta itu. Dengan demikian kelas-kelas ekivalensi dalam partisi itu memuat elemen-elemen semesta yang takterbedakan satu sama lain. Relasi ekivalensi adalah model matematik paling sederhana yang dapat dipergunakan untuk merepresentasikan keadaan di mana elemen-elemen ter­tentu dalam suatu semesta tidak dapat dibedakan satu sama lain, dengan mengingat bahwa relasi “takterbedakan” itu pada dasarnya adalah suatu relasi ekivalensi, yaitu bersi­fat refleksif, simetrik, dan transitif.

Seperti halnya himpunan kabur, konsep himpunan kasar adalah perampatan kon­sep himpunan tegas, dalam arti bahwa himpunan tegas adalah kejadian khusus dari him­punan kasar. Konsep himpunan kasar didefinisikan dengan menggunakan apa yang dise­but ruang hampiran.

Misalkan X adalah suatu semesta yang takkosong, R adalah suatu relasi ekivalensi pada X,  adalah kelas ekivalensi yang memuat  dan  adalah himpunan hasil-bagi pada X yang terimbas oleh relasi ekiva­lensi R, yaitu keluarga semua kelas ekivalensi yang terimbas oleh R pada X. Pasang­an  disebut ruang hampiran, masing-masing kelas ekivalensi dalam X/R dise­but himpunan elementer atau atom dalam K, dan elemen-elemen dalam suatu himpunan elementer disebut elemen-elemen yang takterbedakan dalam K. Dalam setiap ruang ham­piran K, himpunan kosong juga dianggap sebagai himpunan elementer. Setiap gabungan berhingga banyak him­punan elementer dalam K disebut himpunan tersusun dalam K.

Jika A adalah suatu himpunan bagian dari semesta X, maka hampiran bawah dari A dalam K, dengan lambang  adalah

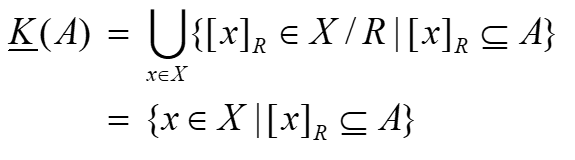
yaitu gabungan semua himpunan elementer yang termuat dalam A. Sedangkan hampiran atas dari A dalam K, dengan lambang  adalah

yaitu gabungan semua himpunan elementer yang beririsan dengan A. Hampiran bawah dari A menyajikan himpunan elemen-elemen semesta yang pasti merupakan anggota himpunan A, sedangkan hampiran atas dari A menyajikan him­punan elemen-elemen se­mesta yang mungkin merupakan anggota himpunan A. Jelas bahwa  Elemen-elemen semesta yang tidak berada dalam hampiran atas dari A adalah elemen-elemen yang pasti tidak merupakan anggota A.

Selisih hampiran atas dan hampiran bawah dari him­punan A dalam K, yaitu  disebut daerah batas dari himpunan A dalam K. Jika  yaitu , maka A merupakan gabungan himpunan elementer dalam K dan disebut himpunan yang dapat dideskripsikan secara tepat dalam K (atau himpunan tegas dalam K). Jika  maka A tidak dapat dideskripsikan secara tepat dalam K dan disebut himpunan kasar dalam K. Dengan perkataan lain, himpunan kasar adalah him­punan bagian dari semesta yang mempunyai daerah batas yang tidak kosong.

Suatu ilustrasi himpunan kasar A dengan hampiran bawah dan hampiran atasnya dalam suatu ruang hampiran disajikan dalam Gambar 5.

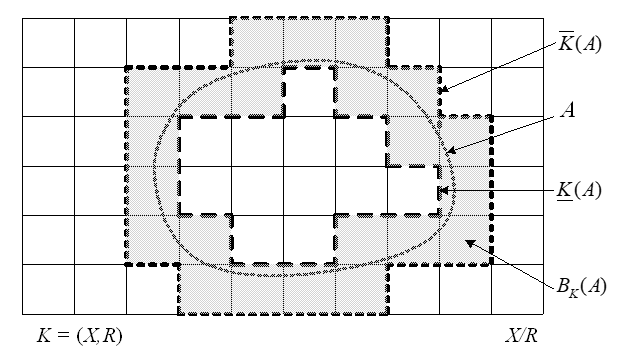
Gambar 5. Himpunan kasar A dengan  hampiran bawah dan hampiran atas dalam ruang hampiran.

Kualitas hampiran dalam suatu ruang hampiran dinyatakan dengan suatu ukuran ketepatan. Bila  adalah suatu ruang hampiran dan A suatu himpunan bagian dari X, maka banyaknya atom dalam  dan  yang disajikan dengan  dan  berturut-turut disebut ukuran dalam dan ukuran luar dari A dalam K. Jika  maka A dikatakan terukur dalam K. Ketepatan hampiran dari A dalam K didefinisikan sebagai bilangan real

di mana  Jelas bahwa  dan  jika A terukur dalam K.

Sebagai contoh,  misalkan ?+ adalah himpunan semua bilangan real positif dan R adalah relasi ekivalensi pada ?+ yang mengimbas partisi (0,1], (1,2], (2,3], (3,4], ? . Dalam ruang hampiran K = (?+, R), selang terbuka (0,r) dalam ?+ di mana  untuk suatu bilangan bulat positif n, mempunyai hampiran bawah

yaitu himpunan elemen-elemen dalam ?+ yang pasti merupakan anggota selang (0,r), dan hampiran atas

yaitu himpunan elemen-elemen dalam ?+ yang mungkin merupakan anggota selang (0,r). Daerah batas dari selang (0,r) dalam ruang hampiran K adalah

yang berarti selang (0,r) adalah suatu himpunan kasar dalam K. Ketepatan hampiran tersebut dalam K adalah

Selang setengah terbuka (0,r] untuk suatu bilangan bulat positif r mempunyai hampiran bawah dan hampiran atas yang sama, yaitu  yang berarti bahwa selang (0,r] merupakan suatu himpunan tegas dan terukur dalam K, yaitu him­punan yang dapat dideskripsikan secara tepat dengan menggunakan himpunan-himpunan elementer (atom) dalam ruang hampiran K tersebut.

Teori Himpunan Kasar telah berhasil diaplikasikan dalam berbagai bidang, antara lain sistem pakar, analisis data, penggalian data (data mining), kedokteran, dll.

5.      Teori Himpunan Lunak

Pada tahun 1999 Molodtsov memperkenalkan konsep himpunan baru yang dise­butnya himpunan lunak (soft sets). Misalkan X adalah himpunan semesta dan P(X) adalah himpunan kuasa dari semesta X. Misalkan E adalah himpunan parameter-parameter. Pa­rameter dapat berupa sifat, atribut, atau karak­teristik dari elemen-elemen dalam X, yang dapat dinyatakan dalam bentuk kata, ungkapan, ka­limat, bilangan real, pemetaan, dsb. Pasangan (F, E) disebut himpunan lunak pada se­mesta X  jika dan hanya jika F adalah suatu pemetaan dari E ke P(X), yaitu  De­ngan demikian, himpunan lunak pada semesta X adalah keluarga himpunan-himpunan bagian dari X yang berparameter. Untuk setiap  himpunan F(e) dalam P(X) adalah himpunan elemen-elemen dalam X yang berparameter e (atau mempunyai sifat / atribut / karakteristik yang mendekati e) dari himpunan lunak tersebut.

Sebagai contoh, misalkan semesta adalah himpunan 10 buah rumah dan E = {mahal, murah, bagus, modern, kuno} adalah himpunan parameter yang berhubungan dengan rumah. Misalkan pemetaan  didefinisikan seba­gai berikut:      Maka (F, E) adalah suatu himpunan lunak pada semesta X tersebut yang dapat dinyatakan sebagai berikut: (F,E) = {  rumah murah =       }, dan da­pat dipandang sebagai karakteristik rumah-rumah itu yang dapat dipertimbangkan oleh seseorang yang akan membeli rumah. Himpunan bagian F(mahal), misalnya, adalah him­punan rumah-rumah dalam semesta X  yang dianggap berharga mahal oleh seorang calon pembeli. Setiap pe­metaan F pada suatu himpunan parameter yang berkaitan dengan rumah akan mengha­silkan suatu himpunan lunak pada semesta X.

Himpunan kabur Zadeh dapat dipandang sebagai himpunan lunak. Misal­kan  adalah himpunan kabur dalam semesta X dengan fungsi keanggotaan  Po­tongan-  dari himpunan kabur  tersebut adalah himpunan bagian tegas dari X, yaitu:

untuk setiap Perhatikan F sebagai suatu pemetaan dari [0,1] ke P(X), yaitu Jika pemetaan F itu diberikan, maka dengan Teorema Dekomposisi dalam Teori Himpunan Kabur dapat diperoleh himpunan kabur yaitu:

untuk setiap  di mana  adalah fungsi karak­te­ris­tik dari himpunan  Maka himpunan kabur  dapat dipandang sebagai himpunan lunak

Beberapa konsep dasar yang berkaitan dengan himpunan lunak, seperti himpunan bagian, komplemen, gabungan, dan irisan, diperkenal­kan oleh Maji, et al. (2003). Aktas & Cagman (2007) memperlihatkan bahwa setiap himpunan kabur dan setiap himpunan kasar dapat dipandang sebagai himpunan lunak. Aplikasi Teori Himpunan Lunak telah dikembangkan secara luas dalam berbagai bidang, misalnya dalam bidang matematika sendiri (analisis, teori peluang, teori ukuran, riset operasi, dsb), dan dalam bidang-bidang lain di luar matematika, seperti fisika, teknik, ke­dokteran, ekonomi, dll.

6.      Penyilangan Dalam Teori-Teori Himpunan

Tumbuhnya berbagai macam Teori Himpunan dalam beberapa dekade terakhir ini untuk menyelidiki berbagai gejala ketidaktegasan itu telah memperluas Teori Himpunan (Set Theory) menjadi Teori-Teori Himpunan (Set Theories) mengenai berbagai macam himpunan seperti diuraikan di atas. Hal itu memotivasi para matematikawan untuk menyilangkan atau menggabungkan konsep-konsep yang relevan dalam Teori-Teori Himpunan itu menjadi teori-teori baru yang lebih luas dan lebih kaya.

D. Dubois dan H. Prade (1990) misalnya, mengawinkan Teori Himpunan Kabur Zadeh de­ngan Teori Himpunan Kasar Pawlak untuk melahirkan dua buah himpunan hi­brid yang baru, yaitu himpunan kabur kasar dan himpunan kasar kabur, dengan tetap memperta­hankan ciri khas dari masing-masing himpunan. Jika konsep hampiran bawah dan ham­piran atas dari Teori Himpunan Kasar Pawlak diterapkan pada suatu himpunan kabur, maka hasilnya adalah himpunan kabur kasar (rough fuzzy sets). Dengan memper­luas re­lasi ekivalensi yang dipakai untuk mendefinisikan ruang hampiran dalam Teori Him­punan Kasar Pawlak menjadi relasi similaritas kabur akan dihasilkan himpunan kasar ka­bur (fuzzy rough sets).

Penyilangan antara Teori Himpunan Kabur Zadeh dan Teori Himpunan Lunak Molodtsov dirintis oleh Maji et al. (2001), yang memperkenalkan himpunan campuran baru, yaitu himpunan lunak kabur. Himpunan kuasa P(X) dari semesta X dalam Teori Himpunan Lunak Molodtsov diperluas menjadi himpunan kuasa kabur  yaitu him­punan semua himpunan kabur dalam semesta X. Maka diperoleh himpunan lunak kabur (fuzzy soft sets) pada se­mesta X, yaitu pasangan (F, E) yang terdiri dari pemetaan  dan himpunan parameter E.

Mengikuti pola penyilangan yang dirintis Dubois & Prade, Feng et al. (2010) menggabungkan Teori Himpunan Kasar Pawlak dan Teori Himpunan Lunak Molodtsov untuk menghasilkan dua buah himpunan campuran yang baru, yaitu himpunan lunak ka­sar dan himpunan kasar lunak. Apabila konsep ruang hampiran dalam Teori Himpunan Kasar  Pawlak diterapkan pada suatu himpunan lunak, maka hasilnya adalah himpunan lunak kasar (rough soft sets). Feng et al. juga memperlihatkan bahwa relasi ekivalensi  yang dipakai untuk mendefinisikan ruang hampiran dalam Teori Himpunan Kasar Pawlak dapat diganti dengan suatu himpunan lunak sehingga menghasilkan ruang hampiran lu­nak, yang selanjutnya dapat dipergunakan untuk mendefinisikan himpunan kasar lunak (soft rough sets). Apabila ruang hampiran lunak diterapkan pada suatu himpunan kabur, maka hasilnya adalah himpunan campuran baru yang disebut himpunan kabur kasar-lu­nak (soft-rough fuzzy sets).

7.      Penutup

Berbagai gejala kekaburan dan ketidaktegasan yang terdapat di mana-mana dalam realitas kehidupan manusia telah mendorong para ilmuwan dalam beberapa dekade ter­akhir ini untuk mencari terobosan-terobosan baru guna memperkembangkan Teori Him­punan klasik yang sudah tersedia menjadi Teori-Teori Himpunan yang lebih luas dan le­bih kaya seperti diuraikan di atas. Sebenarnya masih ada beberapa teori himpunan tak-tegas lainnya yang tidak dibahas dalam karangan ini. Misalnya Teori Himpunan Kabur Intuisionistik (Intuitionistic Fuzzy Sets) yang dirintis oleh Krassimir T. Atanassov sejak tahun 1986 sebagai generalisasi dari Teori Himpunan Kabur. Pada tahun yang sama (1986) Ronald R. Yager  memperkenalkan Teori Kantong Kabur (Theory of Fuzzy Bags) dengan menggunakan fungsi cacah (counting function) untuk menghitung banyaknya kali suatu elemen muncul dalam suatu kantong (yang seringkali juga disebut multiset, karena memperbolehkan elemen-elemennya muncul lebih dari satu kali). Dapat diperlihatkan bahwa kantong atau multiset itu dapat dipandang sebagai kejadian khusus dari himpunan kasar. Selanjutnya W. L. Gau dan D. J. Buehrer pada tahun 1993 memperkenalkan Teori Himpunan Samar (The­ory of Vague Sets) dengan menggunakan fungsi keanggotaan benar dan fungsi keanggo­taan salah. Aplikasi berbagai macam teori himpunan tak-tegas itu serta silangannya telah merambah ke berbagai disiplin limu, seperti ilmu ekonomi, reka­yasa, ekologi, kedokter­an, dan ilmu-ilmu sosial.

Gencarnya penelitian dan pengembangan dalam bidang teori-teori himpunan tak-tegas akhir-akhir ini telah melebarkan jalan bagi ilmu pengetahuan untuk memasuki dan menggeluti fenomena ketidaktegasan dalam realitas dunia nyata. Kemungkinan yang luas untuk menyilangkan teori-teori himpunan tak-tegas itu telah membuat teori-teori baru itu menjadi semakin kaya dan mempunyai daya jangkau terhadap gejala ketidaktegasan yang semakin luas. Quo vadis Teori Himpunan? Teori-teori himpunan pada saat ini sedang bergerak menuju realitas dunia nyata masa depan yang kekaburan dan ketidaktegasannya sedikit demi sedikit semakin dapat dikuasai oleh manusia dan ilmunya. Teori-teori him­punan sekaligus juga menantang para ilmuwan di masa depan untuk mencari cara-cara yang cerdas guna menyatukan berbagai teori himpunan yang masih terpisah-pisah itu menjadi suatu teori himpunan universal yang bersifat umum, dengan Teori Himpunan Cantor sebagai kejadian khususnya.

*Artikel ini pernah dimuat di Buku Melayang dari Masa Depan; 50 Tahun Jozep Edyanto, 2013. Ijin tayang ulang sudah diberikan oleh pihak penerbit.

Daftar Rujukan

 Aktas, H. and Cagman, N. 2007. “Soft Sets and Soft Groups.” Information Sciences, 177: 2726 – 2735.

 Dubois D. and Prade, H. 1990. “ Rough Fuzzy Sets and Fuzzy Rough Sets.” Int. J. of General Systems, 17: 191 – 209.

 Feng, F. et al. 2010. “Soft Sets Combined with Fuzzy Sets and Rough Sets: A Tentative Approach.” Soft Computing, 14: 899 – 911.

 Maji, et al. 2001. “Fuzzy Soft Sets.” J. Fuzzy Math. 9: 589 – 602.

 Maji, et al. 2003. “Soft Set Theory.” Comput. Math. Appl., 45: 555 – 562.

 Molodtsov, D. 1999. “Soft Set Theory – First Results.” Comput. Math. Appl., 37: 19 – 31.

 Pawlak, Z. 1982. “Rough Sets.” Int. J. Inform. Comput. Sci., 11: 341 – 356.

 Zadeh, L. A. 1965. “Fuzzy Sets.” Inform. Control, 8: 338 – 353.